The new, Open Source implementation of R (www.r-project.org) now includes an object-oriented mosaicplot() on which future work will build. A newly-released R package, vcd extends mosaic displays, and implements many of the graphical methods from Visualizing Categorical Data
Consider Table 1, which shows data on the relation between hair color and eye color among 592 subjects (students in a statistics course) collected by Snee (1974). The Pearson X2 for these data is 138.3 with 9 degrees of freedom, indicating substantial departure from independence. The question is how to understand the nature of the association between hair and eye color.
Table 1: Hair-color eye-color data
Hair Color
Eye
Color BLACK BROWN RED BLOND | Total
|
Brown 68 119 26 7 | 220
Blue 20 84 17 94 | 215
Hazel 15 54 14 10 | 93
Green 5 29 14 16 | 64
--------------------------------------------+------
Total 108 286 71 127 | 592
For these data, the marginal proportions are:
Marginal proportions
Black Brown Red Blond
0.1824 0.4831 0.1199 0.2145
This gives the first mosaic display:
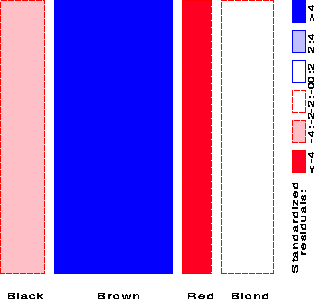
Fitted frequencies
Black Brown Red Blond
148.00 148.00 148.00 148.00
Standardized Pearson residuals
Black Brown Red Blond
-3.29 11.34 -6.33 -1.73
and these values are shown by color and shading as shown in the legend.
The high positive value for Brown hair indicates that people
with brown hair are much more frequent in the population than
the Equiprobability model would predict.
Marginal proportions
Brown Blue Hazel Green TOTAL
Black 0.6296 0.1852 0.1389 0.0463 1.0
Brown 0.4161 0.2937 0.1888 0.1014 1.0
Red 0.3662 0.2394 0.1972 0.1972 1.0
Blond 0.0551 0.7402 0.0787 0.1260 1.0
This gives the second mosaic display:
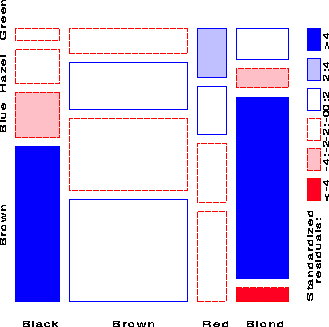
Standardized Pearson residuals
Brown Blue Hazel Green
Black 4.40 -3.07 -0.48 -1.95
Brown 1.23 -1.95 1.35 -0.35
Red -0.07 -1.73 0.85 2.28
Blond -5.85 7.05 -2.23 0.61
This interpretation is enhanced by reordering the rows or columns of the two-way table so that the residuals have an opposite corner pattern of signs.
Here, this is achieved by reordering the Eye Colors as shown below:

Standardized Pearson residuals
Brown Hazel Green Blue
Black 4.40 -0.48 -1.95 -3.07
Brown 1.23 1.35 -0.35 -1.95
Red -0.07 0.85 2.28 -1.73
Blond -5.85 -2.23 0.61 7.05
Thus, the mosaic shows that the association between Hair and Eye color
is essentially that
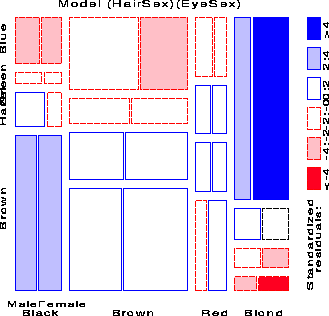
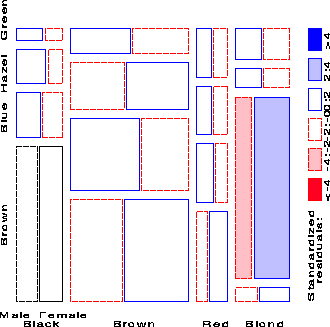
Imagine that each cell of the two-way table for Hair and Eye color is further classified by one or more additional variables--sex and level of education, for example. Then each rectangle can be subdivided horizontally to show the proportion of males and females in that cell, and each of those horizontal portions can be subdivided vertically to show the proportions of people at each educational level in the hair-eye-sex group.
Here is the mosaic for the three-way table, with Hair and Eye color groups divided according to the proportions of Males and Females:
We see that there is no systematic association between sex and the combinations of Hair and Eye color -- except among blue-eyed blonds, where there are an overabundance of females.
For three-way tables, there are three different types of models of "independence" (with several instances each, permuting the variables A, B, and C):
| Model | Log-linear model | Predicted cell probabilities | What the residuals show |
|---|---|---|---|
| Mutual Independence |
[A] [B] [C] | | Residuals show all associations among variables |
| Joint Independence |
[A B] [C] | | Residuals show associations between variable C and combinations of A and B |
| Conditional Independence |
[A C] [ B C] | No closed-form formula | Residuals show associations between A and B, holding C constant |
For higher-way tables, there are many more possibilities.
Moreover, the series of mosaic plots fitting submodels of Joint Independence to the marginal subtables have the special property that they can be viewed as partitioning the hypothesis of Mutual Independence in the full table.
For example, for the hair-eye data, the mosaic displays for the [Hair] [Eye] marginal table and the [HairEye] [Sex] table can be viewed as representing the partition
Model df G2 [Hair] [Eye] 9 146.44 [Hair, Eye] [Sex] 15 19.86 ------------------------------------------ [Hair] [Eye] [Sex] 24 155.20
This partitioning scheme extends directly to higher-way tables.
It is possible, however, for the marginal relations among variables to differ in magnitude, or even in direction, from the relations among those variables controlling for additional variables. The peculiar result that a pair of variables can have a marginal association in a different direction than their partial associations is called Simpson's Paradox.
One way to determine if the marginal relations are representative is to fit models of Conditional Association and compare them with the marginal models. For the running example, the appropriate model is the model [Hair, Sex] [Eye, Sex], which examines the relation between Hair Color and Eye Color controlling for Sex. The fit statistic is nearly the same as for the unconditional marginal model:
Model df G2 [Hair] [Eye] 9 146.44 [Hair, Sex] [Eye, Sex] 15 156.68And, the pattern of residuals is quite similar to that of the [Hair] [Eye] marginal model, so we conclude there is no such problem here.